把大小关系看成一条边。

发现,最长的路径,就是从 \((1,x)\rightarrow(n,y)\) 的这样长度为 \(m\) 的路径。
现在一共有 \(m+1\)
种不同数值,所以每条路径只会有 \(1\)
处可以选择比正常大 \(1\) 的数值。
所以假如要选某一个点作为 \(+1\)
的点,此时,他左上的的点都不能选。
所以可以有以下爆搜的代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| #include<bits/stdc++.h>
using namespace std;
int n,m,ans;
inline void dfs(int x,int down)
{
if(x==n+1) {ans++;return ;}
for(int i=down;i<=m;i++) dfs(x+1,i);
dfs(x+1,max(down-1,1));
}
int main()
{
cin>>n>>m;
dfs(1,1);
cout<<ans<<endl;
}
|
发现这个选的状态可以理解成走格子。
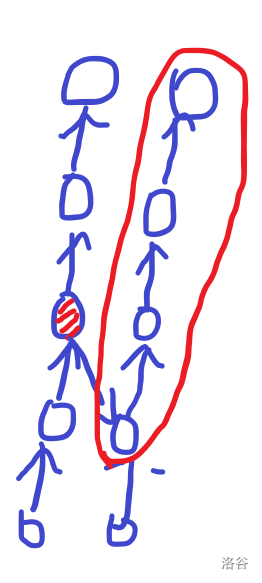
假如上次选的是红色节点,那么红色圈起来的就是可选。
可以选的状态,相当于每次向右下走,接下来向上走能到的节点状态。
那么可以用一条只往 右下,上,走的路径,代表一种状态。
这个代表是双射,证明比较显然。
任何一种状态可以用一条路径表示,这个显然。
一条路径,可以代表一种状态,就是看那一步是向右下走。
\(tips\)
注意这个最下一排,我们要新建一排 虚点使其可以转移。
为了统计最后一列的和,可以新建一排虚点,然后把路径个数和转成到点
\((n+1,m+1)\) 的路径个数。

统计路径大概的 \(dp\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| #include<bits/stdc++.h>
using namespace std;
int n,m,ans;
#define int long long
int dp[1000][1000];
const int mod=1e9+7;
signed main()
{
cin>>n>>m;
dp[1][1]=1;
for(int i=1;i<=m+1;i++) dp[1][i]=1;
for(int i=2;i<=n;i++)
{
dp[i][0]=dp[i-1][1];
for(int j=1;j<=m+1;j++) dp[i][j]=dp[i-1][j+1]+dp[i][j-1], dp[i][j]%=mod;
}
int ans=0;
for(int i=1;i<=m+1;i++) ans+=dp[n][i],ans%=mod;
cout<<ans<<endl;
}
|
把这个斜着的图“转正”。
本质上相当于是一个矩形,有两条线限制,不能经过这两条线的点。
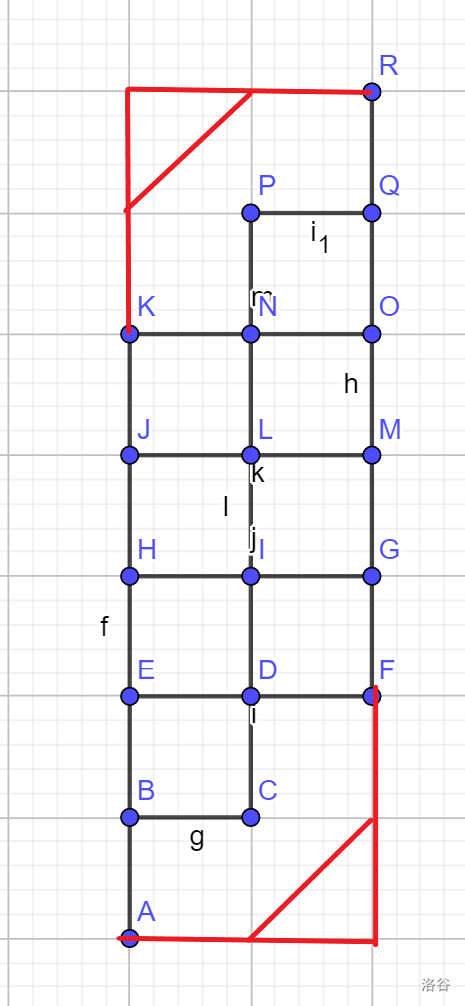
如果只有一条线限制,可以用折线法,构造双射。
如果我们对于每一条线折一次线,会用重复,比如说,我们假设经过
第一条线叫做 \(A\) ,经过第二条线叫做
\(B\)。注意,假如连续经过\(A\ or \ B\) ,我们只算一次。
那么 \(AB\) 。会被 \(A\) 算一遍 ,\(B\) 算一遍。
这时我们要减去 \(AB,BA\)
。此时还会有类似问题 。于是考虑容斥,这个类似前缀容斥。
即对 \(ABAB\cdots\)
这种串进行容斥。
\(tips\)
具体就是每次把一条直线根据另一条直线对称,然后把终点关于“对称后”这条新直线,再次对称。
由于每次问题都可以化归成经过两条直线的路径数,而且直线斜率均为 \(1\),我们可以只维护截距,这样很好计算对称后的坐标,新的截距等你所维护的东西。
折线法代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include<bits/stdc++.h>
using namespace std;
int n,m;
#define int long long
const int mod=1e9+7,N=3e6+10;;
int f[N],finv[N];
inline int qpow(int a,int b)
{
int k=1;
while(b){if(b&1) k=k*a%mod;a=a*a%mod,b>>=1;}
return k;
}
inline pair<int,int> ref(int x,int y,int d){return make_pair(y-d,x+y-(y-d));}
inline int reflect(int a,int b){return a+a-b;}
inline int comb(int n,int m)
{
if(n<0||m<0||n<m) return 0;
return f[n]*finv[n-m]%mod*finv[m]%mod;
}
signed main()
{
cin>>n>>m;n++,m+=2;
f[0]=1;finv[0]=1;
for(int i=1;i<=n+n+m;i++) f[i]=f[i-1]*i%mod;
finv[n+n+m]=qpow(f[n+n+m],mod-2);
for(int i=n+n+m-1;i>=1;i--) finv[i]=finv[i+1]*(i+1)%mod;
int x,y,a,b,ans=0;
x=n-1,y=n+m-1-1;a=-1,b=m;
ans=comb(x+y,x);
for(int j=1;j<=2;j++)
{
x=n-1,y=n+m-1-1;a=m,b=-1;
if(j==2) swap(a,b);
for(int i=1;i<=n+n+m;i++)
{
if(i==1)
{
pair<int,int>pot=ref(x,y,a);x=pot.first,y=pot.second;
}
else
{
if(i&1)
{
a=reflect(b,a);pair<int,int>pot=ref(x,y,a);
x=pot.first,y=pot.second;
}
else
{
b=reflect(a,b);pair<int,int>pot=ref(x,y,b);
x=pot.first,y=pot.second;
}
}
if(i&1)
{
ans-=comb(x+y,x);
if(ans<0) ans+=mod;
}
else
{
ans+=comb(x+y,x);
if(ans>=mod) ans-=mod;
}
}
}
cout<<ans;
}
|



