cf1515F & cf1515G

cf 1515F

题意

Link

题解

考场时候没时间想了，毕竟D 耽误了我 1h+ 只是因为 while 打成了 if 。。。

首先这个题比较神奇的地方应该是他除了 \(\sum a_i<(n-1)x\) 其余情况都有解。

我胡一个证明吧。

也就是证明 \(sum \ge (n-1)x\) 必然有解。

• 归纳法，n=1时候显然成立，下面就是证明 \(n=t\) 可以转移到 \(n=t-1\) 的状态。

• 首先如果存在 \(a_i\ge x\),那么 \(i\) 随便连都满足。

• 否则 \(\forall a_i< x\),如果不存在 \(a_i+a_j\ge x\)，那么\(\sum_{i=1}^{n-2}a_i<(n-2)x,a_n+a_{n-1}<x\)

  所以 \(\sum_{i=1}^{n}a_i<(n-1)x\) 矛盾，所以一定存在 \(a_i+a_j\ge x\)。

---

注意这样的一点，设 \(a_{max}\) 为最大的 \(a_i\)。

如果 \(a_{max}+a_i<x\)，那么不管别的怎么组合，想要救这个 \(a_i\) 都不可能了。

因为 \(a_{max}<x\),每一个 \(a_i<x\) ,合并对于每一个 \(a_i\) 都是劣的。

再根据上面那个结论，所以要是有解，我 \(a_{max}\) 想和谁合并都可以合并。

---

这样我们有了一个做法，维护 \(a_{max}\) 以及每一个\(i\) 能到达的所有点集 。

每次找出 \(a_{max}\) 并且在他属于的那个点集中，随机找一个不在他这个连通块中的。启发式合并。

Tips:

注意 vector 的 clear 不能释放内存！！而deque的pop_back似乎能释放内存。

一定要启发式合并，不要瞎 yy，以为是均摊的。

能到达的点集肯定是有不合法的（已经联通的），注意处理这个地方的逻辑，一定不要图省事。

参考代码

#include<bits/stdc++.h>
using namespace std;
int n,m,x,w;
const int N=3e5+100;
int fa[N];
long long val[N];
inline int gt(int x)
{
    if(x==fa[x]) return x;
    return fa[x]=gt(fa[x]);
}// 并查集
int a[N];
priority_queue<pair<long long,int> >q;
deque<pair<int,int> >v[N];
inline void merge(int x,int y){
    val[x]=val[x]+val[y]-w;
    if(v[x].size()<v[y].size()) swap(v[x],v[y]);
    for(auto d:v[y])  v[x].push_back(d);
    while(!v[y].empty()) v[y].pop_back();
    fa[y]=x;
}//启发式合并 deque
signed main(){
    ios::sync_with_stdio(false);
    cin>>n>>m>>x;w=x;
    long long sum=0;
    for(int i=1;i<=n;i++) cin>>a[i],sum+=1ll*a[i];
    if(sum<1ll*(n-1)*x) cout<<"NO\n",exit(0);
    // 判断无解
    for(int i=1;i<=n;i++) fa[i]=i,val[i]=a[i];
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        v[x].push_back(make_pair(y,i));
        v[y].push_back(make_pair(x,i));
    }
    for(int i=1;i<=n;i++){
        q.push(make_pair(val[i],i));
    }
    cout<<"YES\n";
    for(int ii=1;ii<n;ii++){
        int i=q.top().second,id=gt(i);q.pop();
        // 取出最大值，当然我们只在并查集根节点出统计即可。
        if(i!=id) {ii--;continue;}
        pair<int,int> y=v[id].back();
        v[id].pop_back();
        if(id==gt(y.first)){// 处理不合法。
            while(gt(v[id].back().first)==id) v[id].pop_back();
            y=v[id].back();
            v[id].pop_back();
        }
        cout<<y.second<<endl;
        merge(gt(i),gt(y.first));
        q.push(make_pair(val[gt(i)],gt(i)));
    }
}

---

---

---

cf 1515G

题意

Link

题解

首先注意，我们不管咋走最后都要回到这个点。

所以我们走的一定是一个回路，可以是不简单回路。

所以以下讨论都在一个 scc 中讨论。(毕竟一个环必然是一个 scc，同时如果这个点不在scc中，他只可能权值为0)。

Lemma 1

不管 \(\bmod\) 什么，如果从 \(A\rightarrow B\) 有一条权值和为 \(x\) 的路径，一定存在一条从 \(B\rightarrow A\) 权值为 \(-x\) 的路径。

由于是scc，设 \(B\rightarrow A\) 之间有一条权值为 \(y\) 的路径。（\(y\) 具体是什么并不重要）

假设当前 \(\bmod m\)，我们从 \(B\) 开始，在 \(A,B\) 之间往复走 \(m-1\) 次，最后一次到 \(A\)。

此时权值和为 \((m-1)(x+y)+y \equiv (m-1)x\equiv -x\bmod m\)。

qed

---

所以我们现在可以神不知鬼不觉地从 \(A\) 跑到任意一个 \(B\) ，然后在 \(B\) 那里随便走几个圈，然后神不知鬼不觉地回来。

（因为 \(A\rightarrow B\) 权值为 \(x\),存在 \(B\rightarrow A\) 权值为 \(-x\)，这么一来一回相当于，中间的具体从 \(A\) 到 \(B\) 怎么走的不用管了。

那么我们现在能走出的圈的权值，只可能是所有简单圈的权值，通过线性运算得出的权值。

由于裴蜀定理，现在能表示出的圈的权值，都是 \(\gcd(l_1,l_2,\cdots,l_k)\) 的倍数。\(l_i\) 表示简单环的长度。

怎么找到所有简单环也是个问题。

建出dfs 树后，一条非树边连接的 \((u,v,w)\) 产生了一个权值为 \(dep_u+w-dep_v\) 的环。

这还不够，因为还存在两条非树边产生的环。但冷静思考一下，这个环的长度可以用两个非树边连接的环长度和表示。

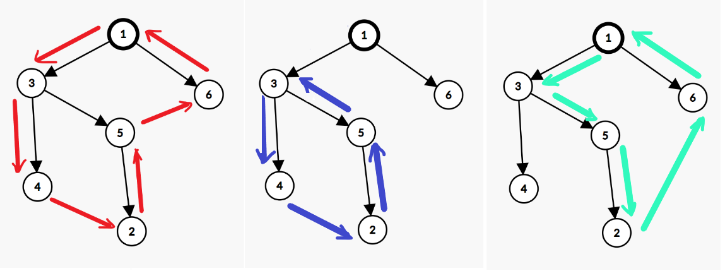
如图所示，红色可以由蓝色，绿色相加而得，注意边的正反。

由于我们一直强调的线性表示，所以在 \(\gcd\) 的角度下，蓝色和绿色在一起等价于红色。

我们只要算有一条非树边产生的环的 \(\gcd\) 即可。

\(Code\)

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
const int N=2e5+1000;
vector<pair<int,int> > v[N],e[N];
int cnt,col[N],dfn[N],low[N],c;
stack<int>s;bool vis[N];
inline void tarjan(int x){
    dfn[x]=low[x]=++cnt;
    s.push(x);vis[x]=1;
    for(int i=0;i<v[x].size();i++){
        int y=v[x][i].first;
        if(dfn[y]==0){
            tarjan(y);low[x]=min(low[x],low[y]);
        }
        else if(vis[y]) low[x]=min(low[x],dfn[y]);
    }
    if(low[x]==dfn[x]){
        int y=-1;c++;
        while(y!=x){
            y=s.top();s.pop();
            col[y]=c;vis[y]=0;
        }
    }
}
// 以上为tarjan
int dep[N];
inline int gcd(int a,int b){
    if(b==0) return a;
    return gcd(b,a%b);
}
int g[N];
inline void work(int x){
    vis[x]=1;
    for(int i=0;i<e[x].size();i++){
        int y=e[x][i].first;
        if(vis[y]){
            g[col[x]]=gcd(g[col[x]],dep[x]+e[x][i].second-dep[y]);
        }   
        else {
            dep[y]=dep[x]+e[x][i].second;
            work(y);
        }
    }
}
int q,a,b,u;
signed main(){
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int x,y,w;
        cin>>x>>y>>w;
        v[x].push_back(make_pair(y,w));
    }
    for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
    for(int i=1;i<=n;i++){
        for(int j=0;j<v[i].size();j++){
            int k=v[i][j].first;
            if(col[i]==col[k]) e[i].push_back(v[i][j]);
        }
    }
    // 以上为tarjan
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=n;i++)if(vis[i]==0) work(i);
    cin>>q;
    while(q--){
        cin>>u>>a>>b;
        if(a==0) cout<<"YES\n";
        else if(g[col[u]]==0) cout<<"NO\n";
        else{
            a=b-a;
            if(a%gcd(g[col[u]],b)!=0) cout<<"NO\n";
            else cout<<"YES\n";
        }       
    }
}