有关 Dilworth 定理的简单证明
本文大量参考了这篇博客,如果您是这篇博客的主人,认为我这么“转载”不妥,请联系我删除我这篇博客。
由于我现在是一名高中生,可能下面的表述不是十分严谨,如果您想看一片比较严谨的证明可以去 wiki 查看
part 1 定理内容
Dilworth 定理 (Dilworth's theorem) 主要说明了覆盖一个 dag 最少需要的不交的链的条数等于最长的反链长度。
此处的覆盖指的是点覆盖。
- 反链指的是选取一个集合 \(S\)
,\(S\)
中任意两个点不可互达,如图所示,点 1,2,3 构成了一个反链集合
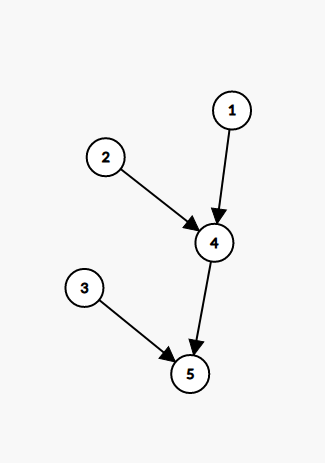
注意这里的链、反链的定义没有要求是连续的,在此图中我们仍可以选择类似 {1,4},{3},{2,5} 这三条链的集合来覆盖这个图上的点。
part 2 证明
我们考虑如何描述一个链划分。
建出二分图 \((U,V,E)\)。对于一个dag到达关系,即偏序关系 \((x,y)\),\(x\prec y\),我们从 \(U\) 的 \(x\) 点,向 \(V\) 的 \(y\) 点连一条边。
现在大抵的思想是先把 \(|U|=|V|\) 个散点拿出,然后根据偏序关系连边。
这样可以观察出由于一个点只能在一个链中,所以可以想到合并两条相接的链可以看作在二分图上匹配。
对于一个匹配,\(M\),如果 \(x\) 是匹配点,记 \(p_x\) 是 \(x\) 的另一个匹配点。
我们考虑沿着某个没有匹配的 \(x\in V\) 开始,接下来跳转到 \(y=x\in U\) ,即当前编号为 \(x\) 在左边集合即 \(U\) 的点。
如果当前点可以匹配到 \(p_x\) 那么接着匹配,此时我们在这个链集合加入了边 \(x\rightarrow p_x\)。
考虑由于偏序关系,不可能产生环,所以以一个点开始的匹配关系,在原图一定可以与一条链一一对应。
考虑我们希望最小化链的个数,也就是最大化链中的边的个数,所以我们希望最大化匹配的个数。
所以最小链覆盖的个数是 \(\text{min chain cover = }|V|-|M|\),\(M\) 为构建出的二分图的一个最大匹配。
接下来我们考虑最小链覆盖 \(C\) 一定大于等于最长反链长度。
考虑反证法,如果 \(|C|< |L|\),同时 \(L\) 中元素在 \(|C|\) 必然属于两两不同的链,显然这样不可能。
\(|L|\leq |C|\)。
考虑 \(L\) 的下界,我们期望 \(L\) 尽可能大,这个上界可以达到,另外我们知道 最大匹配 = 最小点覆盖,所以对于一个 \(M\),我们构造出对应的点覆盖,然后我们选取 不在 点覆盖中的点,这个下界是 \(n-|M|\) ,因为可能有的点即在左面又在右面。。。
直接确定答案。
个人感觉这个东西的难度很大,或者说我个人认为这个定理十分美丽。
感觉有人就是看了个结论,或者,只是看了代码很短就写这个。。。很是没意思讲道理。。。
并且我觉得你知道是反链后,dp也不是第一次看就能看出来的,,也没有那么显然吧。
给出一个例题吧。(模板题。。。)
大概就是把权值拆成点,由于自然形成 dag,直接把问题转换最长反链。
由于顺序是二维偏序,最终的反链形状就是下图这样。

而我们选一个点本质上是在给两个矩形区域涂黑。然后别的点只能在白色位置选。

两边不好考虑,只做一边,另一边作为转移顺序。
记 \(f_{i,j}\) 表示选点 \((i,j)\) 在右下角产生的最长反链长度。
发现本质上是枚举每次转移点,所以维护矩形 Max 即可。
常见的,不知所云的 dp 都是把这个 f 含义转换成矩形 Max 的。
我不太相信很多人多能直接感受到这个dp是在矩形 Max ,就像我不相信很多人能直接感受到完全背包本质上是在压缩转移路径一样。
may be done.
失败的cf出题经历与一道模拟赛题。
给出数 \(n\) 你要求出在 \(n\) 因子这个整除空间中最长反链。
首先不难发现一种构造就是把 质因子个数和(\(d=\prod{p_i^{a_i}},\deg(d)=\sum{a_i}\)) 相等的一组 作为反链。
互不能到达显然了。
可能只是题解的一个解说,题解要证明 \(n\) 的因子一定可以分解成若干个不交的对称因子链。
对称因子链:\(d_1,d_2,\cdots,d_h\),满足 \(\deg(d_1)+\deg(d_h)=\deg(n),d_i=d_{i-1}\times p\)
使用归纳法证明。
设 \(n=m\times p^\lambda\)。
所以假设 \(m\) 可以分解了,对于一条 \(m\) 的对称因子链,\(d_1,d_2\cdots ,d_h\)。
我们打算将这 \(h\) 个数“扩容”因子 \(p\)。
构造 \(d_1,d_1p,d_1p^2,\cdots,d_1p^\lambda,d_2p^\lambda,\cdots d_hp^\lambda\).
\(d_2,\cdots d_2p^{\lambda-1},d_hp^{\lambda-1}\)
\(\cdots\).
如果将 \(\deg(d_i)\) 和 \(p\) 的次数,各看成一维,那么构造情况如下图。

(实际上,由于 \(h\) 可能不等于 \(\lambda\) 所以可能是长方形,最里层的那个可能是 \(d_i,d_{i+1},\cdots d_h\)。)
此时我们给出了一种构造方案。注意对称因子链使得每条链都经过 \(\deg(n)/2\) ,所以此时链的个数是 \(\deg(x)=\deg(n)/2\) 的个数。
考虑 dilworth 的含义是反链长度小于等于任意链覆盖个数。
只要能够取等,那么该反链就是最长反链,该链覆盖就是最小链覆盖。
而恰好,开头说了这个可以构造出,互不整除的结构。
所以成立。
得出结论一种合法的最长反链构造就是 \(\deg(x)=\deg(n)/2\) 的全体 \(x\) 。
试看看,构造的结论是什么?
当然是 \(\deg(x)=\frac{n+n+n}{2}\),所以ban掉了。