Goodbye Xinchou
.只写了A,B,C.
A是个trivial的题。
B 张飞卷精兵。
大概就是考虑到这个 \(2^n\) 恰好形成了一个 \(n\) 层的满二叉树。
考虑我们如果钦定左儿子胜利的话,那么我们本质上确定了每个的符号。
但是如何才能合法呢?
如下图,这是一颗决策树。
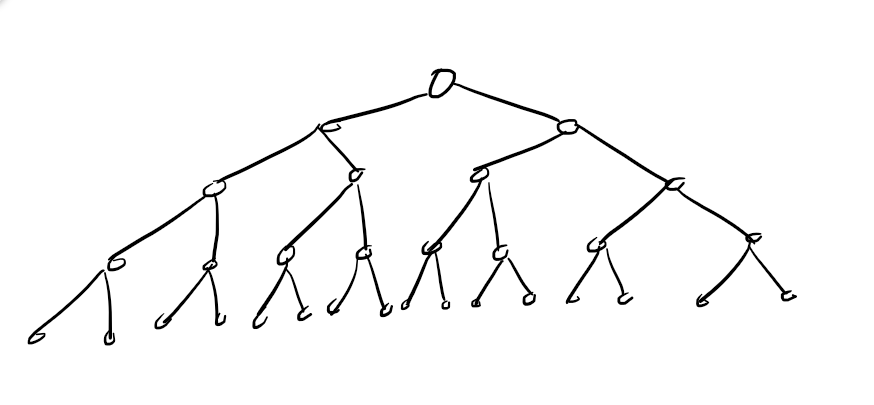
每个节点最后应该是一直走左儿子得到的。
如图:
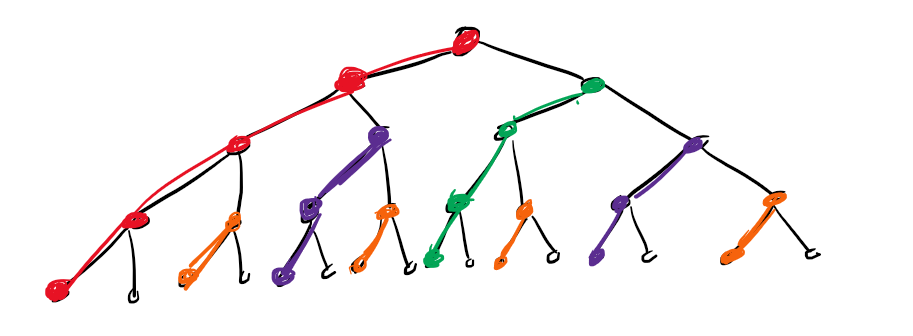
既然我们已经订好了这些东西,我们已经确定了每个数怎么填合法(在根的区间最大),也已经知道如果给出一种填数方案,答案是什么。接下来只需要确定策略即可。
这是我们忽然发现,如果这是一个 \(1,2,\cdots,2^n\) 的序列,那么 \(2^n\) 没人能打得过。(\(\sum_{i=1}^{2^n-1}2^i=2^{2^n}-1\))
所以我们对这个决策树剥根。发现剥完根,会出现一堆“孤儿”,此时我们希望答案最小,也就是这些孤儿的权值尽可能大,这正和我们需要在根最大这个限制不谋而合,我们取出 \(n\) 个最大的数减去。
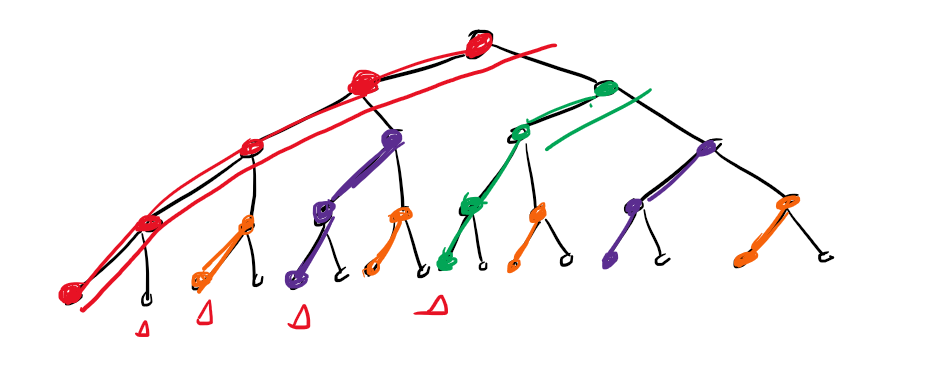
我们再次剥去根后,会产生新的一些子树,但是此时我们便依旧希望这些尽量小。
考虑我们其实陷入了与原问题同样的境地,仔细思考,不难发现我们把最大的数放入最大的子树这个贪心也是没问题的。
因为我们能够尽可能多的减去较大的数,这样一定更优,考虑(\(\sum_{i=1}^{2^n-1}2^i=2^{2^n}-1\))。
所以我们现在递归到了若干子问题。
此时深度一样的子树地位相同,所以 \(\mathcal{O(n^2)}\) 的暴力呼之欲出。
观察性质/暴力维护个数均可以做到 \(\mathcal{O(n)}\) 的。
C 赵云八卦阵
被xor教育(1/100)
首先我们不难发现删除无用。
\(\text{[a,b,c]}\to \text{[a,b xor a,c]}\to \text{[a,bxor a,c xor b xor a]}\to \text{[a,b,c xor b xor a]}\to \text{[a,b,c xor a]}\)
接下来问题转变为每个数可以是前缀异或出来的,问最长上升子序列。
普通的 \(f_i\) 表示到 \(i\) 最长是 \(f_i\) 的 dp没有了出路。
考虑 \(f_{i,j}\) 表示到 \(i\) 长度是 \(j\) 的子序列末尾最小是 \(f_{i,j}\)。
使用线性基转移较为容易做到 \(\mathcal{O(n^2\log w)}\)。
这是考虑,我都线性基了,那么不是基底的数有啥用呀?
对呀如果我们能用前面的表达出 \(b_i\) 那么这个 \(b_i\) 岂不就等价于 \(0\)??
的确的。
发现最终只有 \(\log w\) 段,那么一个很自然的 \(n\log^2w\) 的dp呼之欲出。
其实也没有那么显然把,就是考虑我们记录 \(f_i\) 表示到当前,长度为 \(i\) 的子序列最后的最小是 \(f_i\)。
单点转移就考虑如果 \(f_i\) 加入了一个会怎么样,由于是xor,\(f_i\) 能被新的基表达出来,那么我们只需要找到一个大于 \(f_i\) 而且包含当前 \(b_k\) 的最小的在基里的数。
这个可以把基消成对角基来处理。 \[ \begin{bmatrix} 1&0&0&\cdots&0&\vec b_0\\ 0&1&0&\cdots&0&\vec b_1\\ 0&0&1&\cdots&0&\vdots\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&\cdots&\cdots&\cdots&1&\vec b_{n}\\ 0&\cdots&\cdots&\cdots&\cdots&\vec b_i \end{bmatrix} \] 这样如果当前这位 第 \(k\) 位是 \(0\) 我们直接把低于这位的抹0,然后把这位变成 \(1\)。
否则我们也直接抹0,加上1,然后考虑无论前方什么样子,如果能组成 \(b_k\) 那是最好的,不用管了。
否则我们把 \(b_k\) 这个0再变成1,这样一定合法, 为什么最小?考虑本质上我们只是加了一个 \(b_k+1\) 位,当然最小了。
整段转移类似,但是需要一个类似 \(\min(\mathrm{rank}_i+(j-i))\) 的区间排名最小值,需要那单调队列维护一下。
这时我们只需要插入对角基的时候更新排名。
这也是比较容易实现的,大体上我们看他原来的和需要消去 \(b_k\)
的并,如果是奇数那么我们必须要让他正确,填上一个 \(b_k\)
,否则不变,这样下来判断奇偶性就可以用 __builitin_parity
\(O(1)\) 计算,当然
__builtin_popcount 也行
所以总复杂度 \(O(n\log n)\)。