FMT
时间过得好快呀。我得一天记录一下呀,要不然真忘了。
part1 fwt 与系数矩阵
通常情况下我们需要保证三个矩阵都是一样的,这样才能让我们进行多次卷积。
比如典中典的xor卷积矩阵:
\[ \begin{bmatrix} 1,&1\\ 1,&-1 \end{bmatrix} \]
但如果只做一次,那矩阵不一样可不可以呢?
如下:
\[ \begin{aligned} F_i=\sum a_{i,j}f_j,G_i=\sum &b_{i,k}g_k,H_i=\sum{c_{i,j}}h_j\\ f\oplus g&=h,FG=H\\ \sum_{j,k}a_{i,j}b_{i,k}f_j g_k&=\sum_{j,k}f_jg_kc_{i,w(j,k)}\\ \end{aligned} \]
此时只需要 \(a_{i,j}b_{i,k}=c_{i,w(j,k)}\) 即可。
不需要 \(w(i,j)\) 的交换律。
同时由于 \(w(j,k)\) 的对于位的独立性,我们可以拆开,甚至交换维度,这样只需要考虑二进制运算即可。
更一步,对于任意二元运算(16种),都存在 \(A,B,C\)。
可以通过搜索得出。
part2 集合幂级数
体会了一下集合幂级数,一般定义说的是次幂的含义是集合,而 \(x^{\mathcal A}\) 与 \(x^{\mathcal B}\) 的乘法运算,是次幂的不交并。
换一个视角,用一些代数的语言来描述他,
\(x^{\mathcal S}=\prod_{i\in \mathcal S}x_i\pmod {\prod x_i}\)
我们认为 \(x_i\) 均为变元,也就是依次取模,若存在\(x_i^2\) 这样的项,必定会在该次取模时变成0.
这样在乘法运算上的就是不交并。
part3 子集卷积。
次幂的不交并自然表示了子集的合并。
那么我们能否像前面我们所期待的,将子集卷积这种运算变成位乘呢?
不交并,不交并,说到头也就是并,限制不交可以拿 \(\mathrm{popcount(a)+popcount(b)=popcount(c)}\) 限制。
加法卷积嘛....从而我们引入了占位多项式:
\[ F_z(x)=\sum f_s(z)x^s \]
换句话说,就是我们把原先的 \(\mathbb Z\) 放大到多项式。
这样我们只需先做一次 \(\mathrm{FMT}\),这样就把原先的整数运算,换成对应的多项式运算。
由于 \(\mathrm{popcount(s)}\) 时时刻刻小于等于我们占位多项式每一项的次数,所以可以直接多项式乘法溢出。
但是由于FMT的形式,会暂时产生 \(<\mathrm{popcount(s)}\) 的项,但注意这并不会对正确性产生影响,因为IFMT后的多项式是正确的。
但这让我们需要做多项式的FMT,IFMT。
part3.5 \(n^2\) 多项式
介绍一下 \(n^2\) 多项式技巧。
此下的多项式暂时为形式幂级数。
- \(f(z)=\exp(z)\)
\[ \begin{aligned} f(z)&=\exp(z)\\ &=\sum \frac{z^i}{i!} \end{aligned} \]
将 \(z\) 看成 egf,那么rhs的组合含义是,若划分称大小为 \(i\) 的集合贡献是 \(i![x^i]z(x)\),那么任意egf划分的贡献和。
这个可以钦定每次新选择的是第一个,容易 \(n^2\) dp。
注意我们只不过是借助 egf 考虑问题,所以要先将 \([x^i]z(x)\) 乘上 对应系数,求完的结果也要 除下 对应系数。
- \(f(z)z=1\pmod {x^n}\)
提取第 \(n\) 项系数:
\[ g_n=\sum_{i\le n}[x^i]f(z) z_{n-i} \]
容易看出递推关系。
- \(f(z)=\ln z\)
求导后变成求逆。
part4 多项式符合集合幂级数
很厉害的一个东西。
给出多项式(形式幂?) \(F(x)\),集合幂级数 \(G(s)\)
求 \(F(G(s))\)。
考虑对最高项 \(x_n\) 求偏导,由于是 \(\bmod x_n\) 的,所以最后只剩下常数项(原先的一次项)。
\(F(G)'=F'(G)G'\)
提取仅剩的常数项发现:
\[ [x_n^1]F(G)=[x_n^0]F'(G)\times [x_n^1] G \]
注意,提取的结果是一个 \(n-1\) 元的多项式。
那么这个乘法,应该是 \(n-1\) 维的子集卷积乘法,也就是FMT后的乘法。
这样事实上就递归到了子问题,分别求:
\([x^0_n]F(G)\) 与 \([x_n^0]F'(G)\)。
尽管是分成了两半,但实际上最终要求的不过是:
\(F^{(0)}(G),F^{(1)}(G),F^{(2)}(G),\cdots\)
所以还只是 \(n\) 项,那么合并复杂度:
\[ \begin{aligned} T(n)=\sum (n-k)k^22^k=O(n^22^n)\\ T(n+1)=T(n)+\sum_{k\le n}k^22^k=T(n)+O(2^nn^2) \end{aligned} \]
这也就说明了,\(O(T(n))=O(2^nn^2)\).
整体的算法过程是,首先将 \([x_1^0\cdots x_n^0]F^{(0)}(G),\cdots\) 算出。
向上合并就是将 \(j+1\) 合并到 \(j\) 上面。
如图所示:
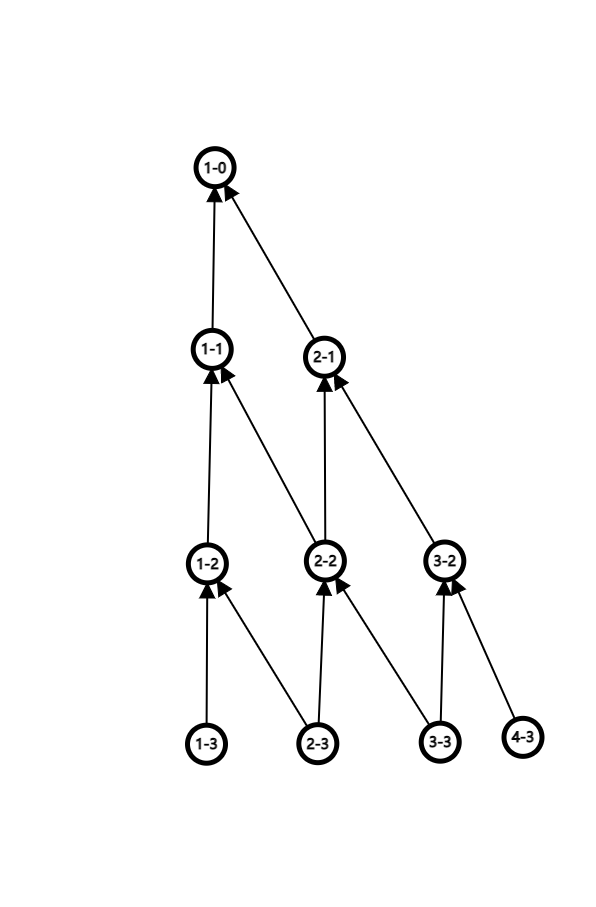
这样终于我们就可以做集合幂的Exp了哦!
Ex
可以发现这个就是把 \(\exp\) 截断了。
那么直接复合即可,代码参考
当时有个地方卡住我了,就是我们 \(j+1\to j\) 的时候合并会多一个 \(x_n\),那么如果我们直接合并上去,如何更新 FMT 结构的值呢?
可以发现事实上我们只不过是shift了一位,所以在这个子空间内,结构是正确的,我们只需要将 \(\mathcal{S}-x_n\) 的信息加上即可。
代码现在看来很短。
例题等待更新。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!